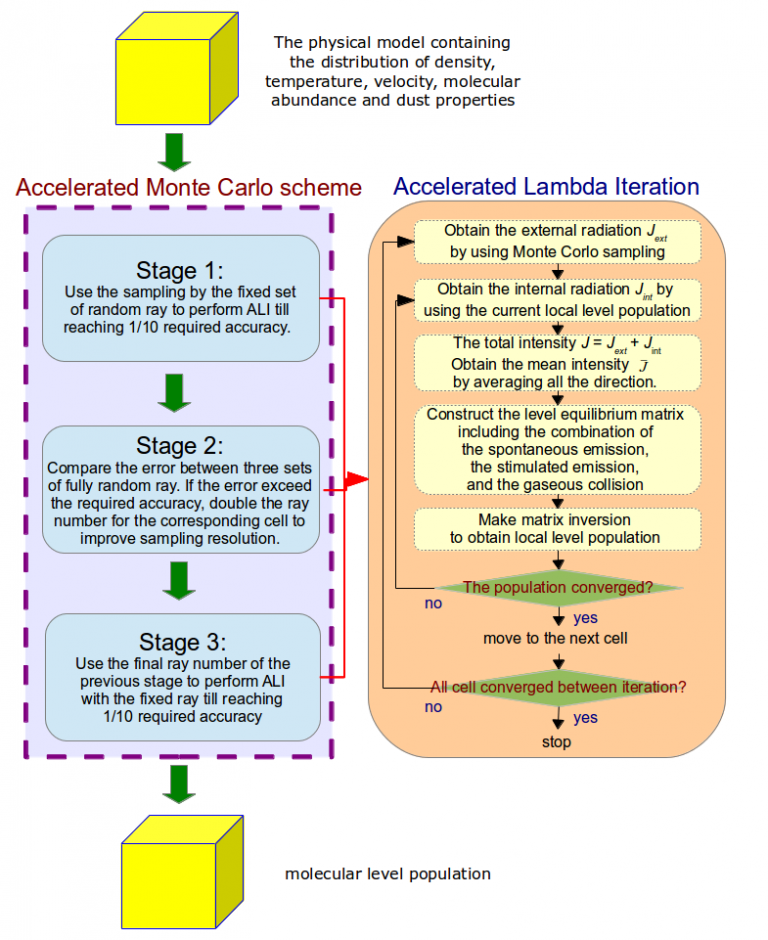
The Monte Carlo method has been widely used for the physics where Knudsen number is relatively large (Kn=λ/∆x>>1) such as long-characteristics radiative transfer. M.R. Hogerheijde and F.F.S. Van der Tak (2000) proposed the accelerated Monte Carlo method (AMC) to preserve the accuracy of the Monte Carlo sampling. The accelerated idea separates two stages to utilize accelerated Lambda iteration (ALI), which was proposed by G.B. Rrbicki and D.G. Hummer (1991), for reaching spatial preliminary consistency at first stage then improve the random sampling resolution to the demanding accuracy at the next stage.
ALI differentiates the intensity inside a cell into the contribution from the internal intensity of the cell Jint and the contribution from the external cell Jext in order to reduce the computational consumption of ray-tracing. Between the iteration, ALI samples Jext once then performs detailed balance calculation to make Jint and population self-consistent.
The AMC scheme was further modified and adjusted for MPI parallelization. A higher signal-to-noise-ratio, compared to the converged criterion (4/3 SNR is adopted), is used for the criterion to diminish the MC error by doubling the ray number. Purely MC error is considered in Stage 2 of AMC without being mixed with iteration error, due to the reason for the parallelization, an additional Stage 3 is to perform fixed ray sampling by the ray number at final Stage 2 and eliminate the error of Lambda iteration. This 3-stages scheme has been validated that the solution can acquire the demanding Monte Carlo error.